简单的回答就是低通滤波器(lpf)允许低频通过,同时阻断高频。最经典的例子就是音频系统中的低音。低通滤波器允许低音传递到大低音,而高通滤波器(hpf)允许高频音传递到高音。甚至可能有一个带通滤波器,允许中音(语音)信号传递到中音扬声器。
在这个例子中,滤波器被用来减轻与扬声器相关的物理效应。低音被传递到一个大型换能器,该换能器能够移动大量空气以提供雷鸣般的低音,而高音则由较小的设备更好地产生。
为了充分理解滤波器的含义和操作,我们需要一个工作的心智模型来区分时间域和频域。我们必须掌握用来描述变频信号的语言,这样我们才能设计并随后评估滤波器的性能。
本文将指出这些基础。它给出了一个理想的一阶低通RC滤波器的仿真结果,然后总结了学生可能遇到的危险。具体来说,就是滤波器在非理想元件的非理想环境中使用时所遇到的问题。
滤波器赖以存在的基础是什么?
传统电子学课程介绍了介于分立晶体管放大器和运算放大器之间的滤波器。遗憾的是,我们没有更多的时间来探索与频域分析相关的丰富语言。事实上,很多学生会尝试在没有使用过频谱分析仪的情况下描述滤波器。在一个相关的,也许同样令人沮丧的情况下,您可能会参加数字逻辑课程,探索如何将低通(抗混叠滤波器)应用于ADC。当你最终完成信号和系统课程时,情况可能会好转。在那之前,请继续阅读这篇文章。
技术小贴士:
低通滤波器通常在模拟数字转换器(ADC)之前使用。低通滤波器用作抗混叠滤波器,防止令人反感的失真形式。这种失真的原因与奈奎斯特采样定理有关,该定理告诉我们,最高ADC输入频率必须小于采样频率的一半。例如,为语音频率设计的系统可以具有6千赫的采样率。任何高于3 千赫的音调都会导致信号失真。
毫无疑问,这是一个复杂的高尔迪结,很可能是你访问这个页面的原因。滤波器是一个具有挑战性的概念,因为它们的应用需要许多相关但基本的概念,如频域分析,带宽,共振,谐波,傅立叶级数和分贝。每一个都很复杂,但可能会让你觉得你是在从消防水管里喝水。
完整的解决方案超出了本文的范围。代替。请允许我给你介绍一些有用的视频。视频1演示了在厨房中遇到的光谱。这是一个近乎完美的声音介绍,为思考滤波器的方式奠定了基础。第二个视频是我的通信系统系列讲座的一部分。它提供了多种思考频谱的方式。它建立在之前的电路I和电路II相量计算的基础上,并使用无线广播探索带宽。最后,它提出了一个涉及低通滤波器、高通、带通和陷波滤波器的仿真。
理想低通滤波器的计算
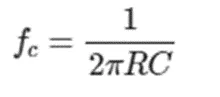
设R = 1.0 kΩ, C = 0.1 uF。结果是-3dB截止约1.6 kHz。在线DigiKey低通滤波器计算器,如图1所示。Multisim 频率扫描的结果,结果在图2中得到进一步支持,图2是使用线性标度呈现的。在这张图中,可以看到幅度从输入的1.0 V下降到输出幅度的0.71 V。
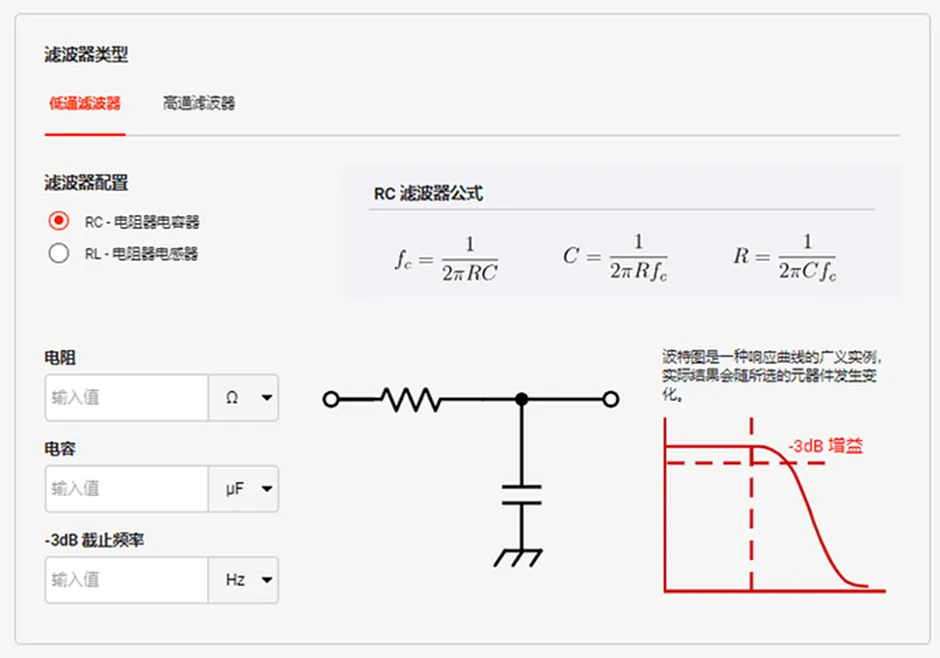
图 1 :R = 1 kΩ和C = 1 uF的DigiKey RC低通滤波器计算器的图像。得到的截止频率约为1.6 kHz。
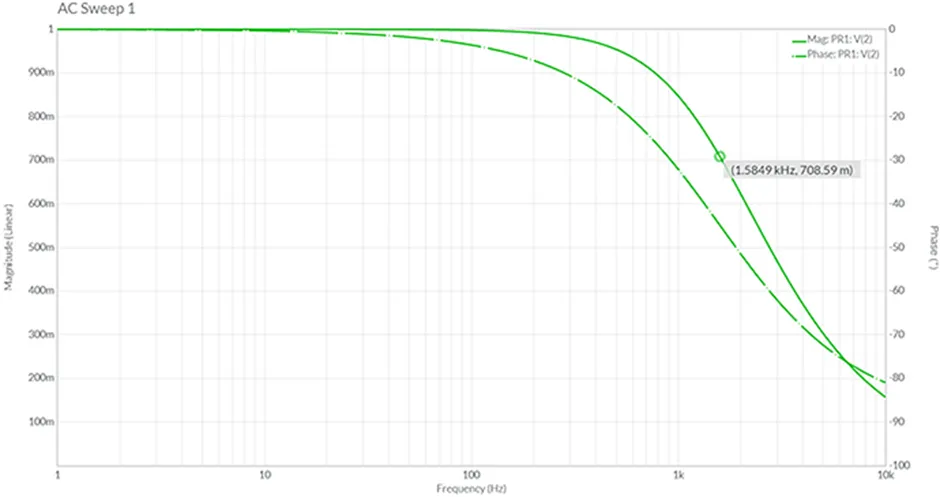
图 2: MultiSim频率扫描的结果显示,在截止频率下,滤波器输出幅度从1.0V下降到0.71V。
技术小贴士:
术语“截止”经常被误解。在低通滤波器的语境中,截止频率是指输出信号为输入信号70.7%。这可以用分贝的形式表示为-3 dB。重要的是要认识到,信号在截止点处显着降低。实际的衰减逐渐从较低的频率开始。
当我们偏离理想低通滤波器时出现的问题
在上一节中,我们在描述滤波器时小心翼翼地使用了“理想”一词。这个术语适用于滤波器本身,也适用于滤波器的使用方式。至于滤波器,术语“理想”意味着组件以理想的方式运行(请参阅技术小贴士)。至于输出,我们假设滤波器与任何负载断开连接。换一种说法,我们假设滤波器的输出正在寻找一个无限的阻抗。
一个典型的错误是将滤波器的输出输入反相运放。假设这个放大器的增益为10,使用1.0 kΩ和10 kΩ电阻对。考虑到运算放大器的虚拟地,滤波器将看到1 kΩ负载。对于低频,滤波器输出幅度不再统一。事实上,对于我们选择的电阻,我们已经形成了一个分压器,在低频时输出减半。我们的截止频率也发生了移位。无需解释,我们应该重新学习Thévenin的定理,开始着手进行AC分析。
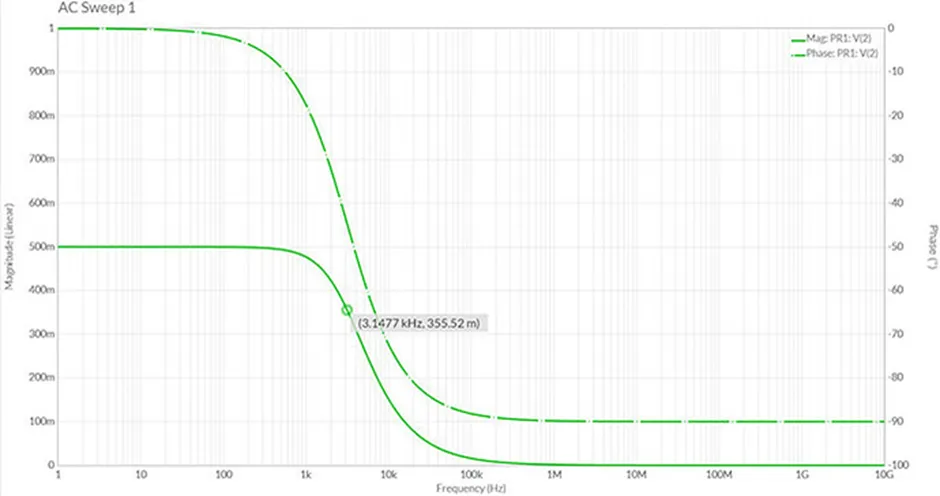
结论
这是理论与现实世界相遇的一个迷人的研究点。低通滤波器一点也不简单。在设计电路时,请牢记这些想法。也许这是许多人称之为艺术的原因。
文章来源:DigiKey得捷
